Lifetime Expected Income Breakeven Comparison between SPIAs and Managed Portfolios

Journal of Financial Planning: April 2014

 

Larry R. Frank Sr., CFP®, is a registered investment adviser and author in Rocklin, California. He has an MBA from the University of South Dakota and undergraduate degree in physics from the University of Minnesota. (Email Larry Frank)

John B. Mitchell, D.B.A., is a professor of finance at Central Michigan University. His research interests include simulation-based retirement planning models, assessment of learning, and derivatives strategies. (Email John Mitchell)

Wade D. Pfau, Ph.D., CFA, is a professor of retirement income at The American College and winner of the Journal of Financial Planning’s 2011 Montgomery-Warschauer Award. He holds a doctorate in economics from Princeton University. (Email Wade Pfau)

Executive Summary

• This paper provides a comparison of total expected lifetime cash flows between single premium immediate annuities (SPIAs) and managed portfolios.
• This analysis shows that assets should be retained and managed in the markets longer than conventional wisdom suggests before the purchase of a SPIA.
• Key factors that encourage annuitization include being older, having greater longevity relative to peers, aversion to holding equities, and higher portfolio fees. 
• The paper concludes with a step-by-step procedure to perform calculations that inform advisers and their clients of the breakeven between SPIAs and managed portfolios using current data.

Retirees have a choice between fully managing their retirement assets, partially annuitizing, and fully annuitizing. Single premium immediate annuities (SPIAs) provide protection against market downturns and above-average longevity; however, these products may not provide inflation protection, and their use often removes the potential for an end-of-life bequest. Managed portfolios provide less certainty about returns but more opportunity for growth and legacy planning. 

Retirees face trying to make the choice between buying a fixed income stream today, with certain loss of purchasing power (non-inflation adjusting annuities are used in this paper’s research because they provide better data and pricing history), or retaining assets and deriving income based on uncertain future market returns. 

Clients and their advisers often ask how they should choose between the two options. This paper seeks to address this issue by determining breakeven asset allocations below which SPIAs provide higher lifetime expected total cash flows. The analysis described here shows how a client’s age is related to the decision. The analysis also shows that other factors impact the choice, including cash flow needs, market returns, and fees. 

The research methodology in this paper looks at the decision from a comparison of the sum of retirement income payments received (the sum of lifetime cash flows). It is important to have adequate retirement income in each individual year of one’s life for as long as that may last, but it may not be as important to retain an ending portfolio value. However, some retirees may wish to leave a bequest by retaining an ending portfolio value. These competing desires define cases where retiree preferences help shape customized solutions.

A Monte Carlo model was developed to track cash flow and portfolio balances by age and allocation. The model was used to determine the effect of prior cash flows on future balances. The Monte Carlo depictions in this paper show a possible range of future cash flows, between “good” returns sequences and “poor” market sequences, over time frames determined by actuarial tables. By comparing the total sum of payments received from a SPIA against the payments expected from a managed portfolio, retirees may then determine which approach can potentially maximize their lifetime consumption. Retirees and their advisers can also determine the age when the cumulative cash flows from a managed portfolio will exceed those from a SPIA and the likelihood of outliving this breakeven age. This paper is an analytical approach to evaluating the choice a retiree faces. Adviser are encouraged to use their own data, now and in the future as data is updated, through a practical application exercise described in the appendix.

Literature Review

Blanchett (2013) noted that cash flows are the most important determinant factor associated with retirement success. Yet, past distribution research has tended not to focus on cash flows, but instead on maximizing the withdrawal rate, which Blanchett observed is more a function of the return (and volatility) data used in research papers.

This paper’s focus is on cash flows that emanate throughout a simulated retirees’ potential lifetime as developed by the methodology presented by Frank, Mitchell, and Blanchett (2011, 2012a, 2012b). The Frank et al. methodology is age-based where annual cash flows may be determined and summed over various expected longevity percentiles from period life tables.

Milevsky (1998) stated, “Consequently, given the low interest rate environment and the long-run propensity for equities to outperform fixed income investments, … a 65-year-old female (male) has a 90 percent (85 percent) chance of being able to beat the rate of return from a life annuity until age 80.” Do those observations hold with lower, or higher, interest rates? Do they hold for other than age 65 retiree ages?

The “annuity puzzle” has been referred to in research at least since Yaari (1965). Economists often question why annuitization is such an uncommon solution for protection from longevity risk. Numerous behavioral and economic explanations have been offered. Benartzi, Previtero, and Thaler (2011) effectively summarized this literature. More recently, Reichling and Smetters (2013) indicated that because health shocks require increased liquidity while simultaneously reducing the present value of remaining annuity payments as a result of heightened mortality, retirees act rationally in their decision to reduce annuity holdings. Kitces and Pfau (2014) also demonstrated that part of the explanation for the beneficial impacts of annuitization on a retirement portfolio can be explained through the implied rising equity glide path of the strategy. 

A Probability-Based 3D Model

Fundamentally, a retiree has three choices about how to provide retirement income. She can (1) annuitize retirement assets, (2) manage those assets, or (3) partially annuitize and manage the balance. Each choice has implications for the total sum of money a retiree may expect over her remaining expected lifetime.¹

The Monte Carlo simulations for this paper were run using a three dimensional (3D) model described by Frank et al. (2011, 2012a, 2012b). This paper provides a practical application of the Frank et al. model to compare total cash flow sums between SPIAs and managed portfolios by allocation exposure to equity and bonds, and by the expected longevity percentile (probability of outliving a particular age) from period life tables.

In the Frank et al. (2011, 2012a, 2012b) 3D model, period life tables and the retiree’s current age are used to set the length of the distribution period each year. The length of the distribution period changes each year throughout the retiree’s lifetime based on subtracting the current age from expected longevity. By being more specific as to the length of the distribution period through the use of period life tables’ longevity percentiles, and rolling simulations that are serially connected through an annual update, it is possible to see more clearly how cash flows change throughout retirement.

A constant probability of failure (POF), which is the percentage of simulations that fail, interacts with the distribution period to determine a withdrawal rate based on a retiree’s current age. Asset allocations (0 percent equity/100 percent bonds through 100 percent equity/0 percent bonds) in 10 percent increments add a third dimension. Note that only those allocations at and below 50 percent equity are depicted in the figures.

The withdrawal rate, given a target POF, is annually recalculated based on each annual distribution period and asset allocation. This paper sets the target POF for all values at 10 percent. However, because the withdrawal rate is annually recalculated, the effective POF is essentially zero, because there is always a portfolio balance (although the annual cash flow would be unknown). In other words, there is a tradeoff between spending and future portfolio balances (Frank et al. 2012a).

The 3D model approach is not a 4 percent rule approach. An important difference between the “4 percent rule” approach and a 3D model approach is that the length of the distribution period, combined with a target POF, determines an appropriate withdrawal rate from the remaining portfolio assets for each year in retirement, regardless of portfolio value. The distribution period is specifically determined by reference to a period life table each year. The distribution period itself may be changed through strategic use of longevity percentiles (LP) such as the median (50th LP) or the 30th LP, in which retirees have a 50 percent chance or 30 percent chance for outliving their life expectancy, respectively (30 percent LP means they outlive 70 percent of their cohort). In other words, the withdrawal rate is determined in the 3D model by the length of the distribution period at a given POF and a given longevity percentile, or LP.² Table 1 summarizes the distribution period lengths.

 

With an established withdrawal rate based on age, the actual dollar amount spent at each age depends on how the markets and past spending have affected the current portfolio value. The annual dollar distribution for spending is the portfolio value multiplied by the withdrawal rate. From the Monte Carlo simulations for remaining portfolio value, the 25th (best one in four) percentile represents “good” market sequences, the 50th percentile is the median sequence, and the 75th (worst one of four) percentile represents “bad” market sequences.

Because managed portfolios usually have management fees, the results compare sensitivity at no fee and 1 percent fees. The no fee data form a baseline for comparison. Fees and taxes (although taxes are not included here) are deducted from annual spending cash flows; however, fees do not adjust the withdrawal rate in this methodology (see Pye 2001). Fees are considered in the managed portfolio for an apples-to-apples comparison, because the SPIA dollar amounts are real SPIA quotes, which implicitly incorporate insurer fees and expenses. It is the sum of these annual cash flows, based on simulation percentile, which this paper compares to the sum of the SPIA payments, over the identical expected longevity from the period life tables.³ These sums are also similarly determined across the third dimension of asset allocation.⁴

Portfolios were assumed to be managed with withdrawal adjustments based on age (Frank et al. 2012b). The withdrawal rate never reaches 100 percent through a limiting function to WR (WR*(1 – 1/n), where n = annually recalculated distribution period) in order to extend portfolio values into any superannuated age that a retiree may reach. Thus, the model is designed so that there is always a portfolio balance to which a withdrawal rate may be applied. In sum, the uniqueness of this paper is the methodology used to track cash flows annually through a portfolio distribution’s lifetime, by simulation percentile and asset allocation, and to compare these cash flows with a SPIA.

Methodology

U.S. market returns were compared to U.S. SPIAs.⁵ Return data were based on four main asset classes from Ibbotson SBBI® (stocks, bonds, bills, and inflation) data from January 1926 through December 2012. Those asset classes were: 30 day T-bills (25 percent bond weight), U.S. intermediate-term government bonds (ITGB) (75 percent bond weight), S&P 500 equities (75 percent equity weight), and U.S. small stocks U.S. (25 percent equity weight). Here is an example for overall weighting using a 60 percent bond/40 percent equity allocation: T-bills (25 percent * 60 percent) = 15 percent; ITGB (75 percent * 60 percent) = 45 percent; S&P 500 equities (75 percent * 40 percent) = 30 percent; U.S. small stocks (25 percent * 40 percent) = 10 percent. Each allocation increment in this paper was asset class weighted accordingly. All returns were converted into inflation-adjusted real returns using SBBI^® U.S. inflation figures. 

The methodology compares an expected total sum of money received between a SPIA and managed assets net of fees, over a given time period, in real terms, and across various asset allocations. The depicted sum of distribution dollars are between the 25th and 75th simulation percentiles to illustrate the most likely boundaries that a retiree may experience throughout the remainder of her lifetime.
Consider Mary, a 65 year-old female living in Texas (a state with no SPIA premium tax). Her starting portfolio value is $1 million. According to a real-time quote from www.immediateannuities.com, she could receive a single life with no payments to beneficiaries monthly payment of $5,170. This compares to a monthly payment of $4,260 from the 3D model at age 65. 

It initially appears that the SPIA will generate more income than the managed account. However, the SPIA is fixed without inflation adjustments, while the cash flow from the managed account is based on inflation-adjusted real returns. To make the numbers comparable, the SPIA income needs to be calculated in real terms using the average 3.04 percent for inflation over the historical period of the dataset. Based on the expected remaining lifespan (N) of 21 years (see Table 1) the inflation-adjusted present value for the SPIA is as follows: ∑₁^N(monthly SPIA*12)/((1+0.030401)ˆN), is $952,664.

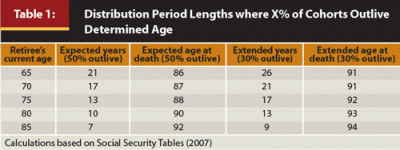
The managed account is expected to generate $1,633,412 of cash flows (40 percent equity, 1 percent fee, including portfolio balance at the end of 21 years) or $1,125,936 (excluding portfolio balance after 21 years). Mary should expect an extra $173,262 ($1,125,926 – $952,664) of purchasing power in current dollars over her lifetime with the managed account, plus a residual balance of $507,476 that may be used for bequest or continuing income.

Figure 1 summarizes the expected total income sums at various allocations, simulation percentiles (25th good sequences, 50th median, and 75th poor sequences), and fees, by various ages that are time slices through the 3D model. In reality, market return sequences will tend to fluctuate around the median values. The graphs on the left side of Figure 1 use expected longevity ages, while the graphs on the right side use extended longevity ages and the resulting distribution periods from Table 1. The difference between Figure 1 and Figure 2 is that in Figure 2, ending portfolio balances are not included in the total lifetime cash flows as a way to equalize the comparison as a retiree gives up her portfolio to buy a SPIA.

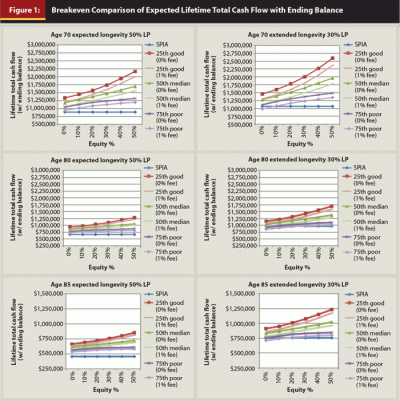
The values in Figure 1 and Figure 2 that lie above the blue SPIA line are above the breakeven value, and the graphed values that lie below the SPIA line are below the breakeven value. For example, if none of the managed portfolio total income sums fall below the annuity breakeven line, with or without ending expected portfolio values, then a SPIA would not be as effective in supporting greater total lifetime cash flows. 

A SPIA does provide protection against living through extensively long poor markets (longevity during bad times). The reason that the SPIA begins to make sense for older retirees is that it is easier to have a significantly long bad market compared to expected lifespan at higher ages, and the variability of remaining life increases relative to expected longevity at higher ages (Mitchell 2010). Additionally, longer time periods allow a greater chance for compounding returns from a managed portfolio to outpace a SPIA. A SPIA also tends to be hampered less at higher ages by the reduced time frame for inflation’s loss of purchasing power effect on the SPIA. However, what cannot be observed in the figures is the risk of SPIA failure resulting from an insurance company failing. Nonetheless, this would also be of lesser concern at older ages as the remaining time horizon shortens.

Figures 1 and 2 illustrate the dynamics of time and portfolio growth, as well as the effect a higher withdrawal rate has on remaining portfolio balances. Think of the Figures as seeking an age where crossover from a managed portfolio to a SPIA may occur. When ending portfolio balances are added back to the total cash flow at the expected longevity age (retiree dies as expected), in all cases the sum total of cash flow from the managed portfolio exceeds the breakeven line representing the cash flow from the SPIA.

The panels in Figures 1 and 2 focus on allocations at and below 50 percent equities, because these are the allocations a retiree would more likely be comfortable holding.⁶ Higher equity allocations have more cash flow, because of the nature of higher returns associated with equities. However, increased volatility associated with increased equity exposure increases the dispersion of results. Portfolio values would most likely fluctuate much closer to the median value, especially if spending adjustments as described in Frank et al. 2011 were used. Barberis (2013, p. 188) described the emotions of spending adjustments as “The intuition is that, upon receiving a negative income shock, the individual prefers to lower future consumption rather than current consumption. After all, news that future consumption will be lower than expected is less painful than news that current consumption is lower than expected. Moreover, when, at some future time, the individual actually lowers consumption, the pain will be limited because, by that point, expectations will have adjusted downwards.” Thus, if a retiree is prepared for an eventuality through discussing the possibility, when the time comes the pain may be more muted.

What Figures 1 and 2 show is the equity exposure a retiree with a managed portfolio must be willing to take as part of her decision to annuitize. If she is comfortable with an equity allocation higher than that indicated in one of the Figures, then she should continue managing assets; if uncomfortable, then she should annuitize. Notice, too, that the SPIA only begins to come into play for those who have a tendency to outlive their cohort and only at advanced ages when they no longer have a long remaining lifespan over which to generate market returns. This is the real purpose of SPIAs; namely, transferring the greater relative longevity risk at advanced ages to SPIA providers.
The insight here is that in order to justify self-managing her portfolio, the retiree needs to have a comfort level with the equity allocations required to do better than a SPIA, and a sense of not likely being in the group of long-lived cohort.

Using SPIA Annual Payout Rates to Determine Breakeven Thresholds

As defined by www.immediateannuities.com, the annual payout rate (APR) is the percentage of the purchase price (premium) that is paid back each year. The APR includes both interest and return of principal. It is not an interest rate. It is significantly higher than the actual interest rate credited to the premium. APR values derived in this paper were the result of a search function, described in the practical application example in the appendix, that solves for an equal value of total cash flow sum for the SPIA with the total cash flow sum for the targeted Monte Carlo simulation value (by allocation and fee level). Using this method, practitioners can compare past, present, or future threshold APR values as demonstrated in Table 2.

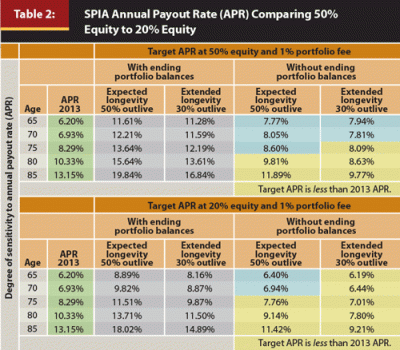
The calculated breakeven APR in Table 2 targets setting the breakeven point for the SPIA line specifically at a 50 percent equities allocation with a 1 percent fee (upper half); or a 20 percent equities allocation with a 1 percent fee (lower half). These targets were used to determine what APR is required as a breakeven comparison for the selected allocation and longevity period.

The basic question retirees and their advisers must ask about a managed portfolio is what equity allocation they are comfortable using. If a retiree is comfortable with an allocation above the SPIA breakeven line, while considering the range of possible future market outcomes between continuous poor markets (75th percentile) and continuous good markets (25th percentile), the retiree should opt to continue to manage her assets outside a SPIA. In this case, she would also evaluate her situation using the insight provided with data that retains the ending portfolio values. If uncomfortable with an equity allocation above the SPIA breakeven line, she should consider buying a SPIA. In the latter case, the evaluation should use data that does not retain the portfolio balances, because those would be given up to purchase the SPIA. 

With this in mind, how does a retiree determine her sensitivity to asset allocation and the SPIA breakeven line through use of the APR as the decision metric? 

Targeted APRs can be used to answer this question. Targeted APRs allows a retiree or an adviser to compare quoted SPIA APRs at any given time to a targeted APR derived from setting a target cash flow breakeven. Yellow highlighted APRs in Table 2 suggest that if a retiree believes she may outlive 70 percent of her cohort, then buying a SPIA at age 65 or older should be considered. Notice though, that if her belief is that she may outlive only 50 percent of her cohort, then age 75 or 80 is when she should consider buying a SPIA, depending on comfort level with equity exposure (50 percent and 20 percent equity, as shown in Table 2). The reader should note that these ages may float over time as market returns data, interest rates governing SPIA payouts, and longevity data change.

What the reader may observe is that the higher SPIA payout, which occurs from the start relative to the lower managed portfolio payout at the start, is overcome over time by the greater real returns that raise the total payout sum for the managed portfolio. Thus, the total real sum of money the retiree receives is greater for the managed account. The extent of the excess depends on the asset allocation. For older starting ages where the SPIA payout is initially higher relative to managed assets, there is not enough time for the combination of inflation (that lowers the real payout of the SPIA) and the effect of real returns (that raises the managed payout) to overcome the SPIA initial payout advantage.

Conclusions

Figure 1 shows for retirees with bequest goals who expect to outlive 70 percent of their cohort (right side), managed withdrawals plus retained value plots above the SPIA breakeven line. Other than in the most pessimistic market expectations and risk aversion situations, managing a portfolio makes sense at all ages. Furthermore, a retained portfolio value still remains to provide income beyond the ending age should the retiree remain living (see Table 1). Portfolio ending value becomes irrelevant when a SPIA is purchased. Thus, Figure 2 comes into use. The panels on the right side of Figure 2 suggest that the earliest a SPIA should be purchased is after age 70, and only for the most market pessimistic and longevity optimistic. The left side of Figure 2 suggests that average longevity retirees should switch to a SPIA around age 80.

By nature, SPIAs require retirees to purchase at some particular age while remaining lifetime is uncertain. This is the mechanism where mortality credits originate. Mortality credits occur when those who die early fund those who live longer than expected. Clearly, someone in poor health should not use a SPIA, because she most likely would not live long enough to recoup her money. Financial planners should point out to their clients that partial annuitization sets that component of a retiree’s income on a fixed trajectory, while the assets retained under management will continue under a future market trajectory. In other words, the intent of the analytical framework outlined in this paper is not an all-or-nothing choice.

The current low interest rate environment suggests that encouraging the purchase of SPIAs prior to age 80 may be misplaced. However, SPIAs may be appropriate if retirees demonstrate a tendency as spendthrifts. In these situations, managed portfolios may not be appropriate to ensure lifetime income.

Retirees concerned about outliving the ages shown in Table 1, and not comfortable with an allocation above the SPIA breakeven line in Figure 2 (right side), should consider purchasing a SPIA based on their current age. However, if they do not believe they will outlive the ages in Table 1 (that is, they are on the left side of Figure 2), then the longevity risk benefits of SPIAs would not be realized, and thus the retiree should not buy a SPIA, especially if they are comfortable with equity allocations above the SPIA breakeven lines. Furthermore, if they retain ownership of their portfolio by not buying a SPIA, then Figure 1 is relevant because ending balances are retained.

Not all risks are equal for individual retirees. If a retiree is at risk of being a spendthrift, then SPIAs will provide income for life and avoid such risk. If there is little risk of long life, transferring assets to a SPIA to insure against this risk is not efficient. At what point does transferring assets to a SPIA make sense? Results suggest that only when the possibility of outliving 70 percent or more of a cohort exists, and then only at elderly ages. For ages younger than 80, assets are best kept within the family, because both inflation and possible future market returns have time to do better than SPIA lifetime sums.

The methodology used for SPIAS in this paper may also be used to evaluate decisions between a pension lump sum offer versus accepting pension payments for life (no COLA), which is comparable to a SPIA. A factor not considered in this paper is that retirees should consider the business risk of the insurance company. SPIA payments should not be considered risk free. Because insurance companies issuing SPIAs invest in the same markets as do the bond portions of managed portfolios, if the retiree’s concern is doing well in continued poor markets, then risk increases that the insurance company will be unable to continue a SPIA established during better times. Ultimately, retirees and their advisers must ask whether the firm will remain in business as long, or longer, than the retiree is alive.

Serial connection of the simulations reflects real life when one considers how subsequent annual reviews are impacted by prior retiree decisions. The difference is that the series of simulations use the same data set. In real life, each annual review would update the data set, which would slightly adjust those simulations going forward (Mitchell 2013). This also has the effect of having the retiree make small adjustments over time, rather than making larger adjustments later.

The methodology introduced in this paper is not the final answer. Readers should not rely on today’s tables and figures. These tools are meant to illustrate the methodology and decision making that requires dynamic insight. Using data known in the future, and the practical application process described in the appendix, future breakeven points will emerge for decision making at that time when all the factors have stochastically changed. Finally, further research is needed to look into possible combinations of partial annuitization over time and/or the use of longevity annuities (deferred income annuities or DIAs), which do not pay out unless a later age is reached. 

Endnotes

1. The term “her” is used because the data and calculations in this paper are based on females, presumably the most at risk for outliving resources.
2. The withdrawal rate increases slightly each year because the distribution period shortens, due to a slightly shorter expected longevity from the period life tables. This simulates the retiree aging and the dynamics of changing life expectancy conditional on age.
3. Longevity data is from the Social Security (2007) period life tables (current table is available at www.ssa.gov/OACT/STATS/table4c6.html). The Annuity 2000 table was also evaluated.
4. Market data are historical averages calculated through year-end 2012. SPIA data are from 2013. These comparisons will, of course, change over time as market returns, SPIA rates, and life tables are updated, as all are stochastic in nature. Clients’ ages and portfolio values will also be a part of the annual update process in a dynamic model, reflecting actual data and spending events in life.
5. Current SPIA payouts were obtained from Immediate Annuities (www.immediateannuities.com). Past data sets for all ages during a higher interest rate era were incomplete. Future cash flows from the SPIA payouts were discounted at the same inflation rate used to convert SBBI returns to real returns so the same discounting factor was applied to all data.
6. Graphs for other ages, annuity tables, equity allocations, etc., may be found at ssrn.com/abstract=2352252.

References

Barberis, Nicholas C. 2013. “Thirty Years of Prospect Theory in Economics: A Review and Assessment.” Journal of Economic Perspectives 27 (1): 173–196.

Benartzi, Shlomo, Alessandro Previtero, and Richard H. Thaler. 2011. “Annuitization Puzzles.” Journal of Economic Perspectives 25 (4): 143–164.

Blanchett, David M. 2013. “The ABCDs of Retirement Success.” Journal of Financial Planning 26 (5): 38–45.

Frank, Larry R., John B. Mitchell, and David M. Blanchett, 2011. “Probability-of-Failure-Based Decision Rules to Manage Sequence Risk in Retirement.” Journal of Financial Planning 24 (11): 44–53.

Frank, Larry R., John B. Mitchell, and David M. Blanchett. 2012a. “An Age-Based, Three-Dimensional Distribution Model Incorporating Sequence and Longevity Risks.” Journal of Financial Planning 25 (3): 52–60.

Frank, Larry R., John B. Mitchell, and David M. Blanchett. 2012b. “Transition through Old Age in a Dynamic Retirement Distribution Model.” Journal of Financial Planning 25 (12): 42–50.

Kitces, Michael E., and Wade D. Pfau. 2014. “The True Impact of Annuities on Retirement Sustainability: A Total Wealth Perspective.” Retirement Management Journal, forthcoming.

Milevsky, Moshe A. 1998. “Optimal Asset Allocation Towards the End of Life Cycle: To Annuitize or Not to Annuitize?” The Journal of Risk and Insurance 65 (September): 401-426.

Mitchell, John. B. 2010 (October). “A Modified Life Expectancy Approach to Withdrawal Rate Management.” Paper presented at the Annual Meeting of the Academy of Financial Services, Denver, Colorado.

Mitchell, John B. 2013 (October). “Retirement Withdrawals: The Historic Return Dilemma.” Paper presented at the Annual Meeting of the Academy of Financial Services, Chicago, Illinois.

Pfau, Wade D. 2012. “Capital Market Expectations, Asset Allocation, and Safe Withdrawal Rates.” Journal of Financial Planning 25 (3): 36–43.

Pye, Gordon B. 2001. “Adjusting Withdrawal Rates for Taxes and Expenses.” Journal of Financial Planning 14 (4): 126–136.

Reichling, Felix, and Kent Smetters. 2013. “Optimal Annuitization with Stochastic Mortality Probabilities.” Congressional Budget Office Working Paper 2013-05. www.cbo.gov/publication/44374.

Yaari, Menachim. 1965. “Uncertain Lifetime, Life Insurance, and the Theory of the Consumer.” Review of Economic Studies 32 (2): 137–50.

Citation

Frank, Larry R., John Mitchell, and Wade Pfau. 2014. “Lifetime Expected Income Breakeven Comparison between SPIAs and Managed Portfolios.” Journal of Financial Planning 27 (4) 38-47.